Postanowiłam sprawdzić w praktyce, jak się mają teoretyczne wyliczenia złożoności obliczeniowej algorytmów do rzeczywistych wyników uzyskiwanych w kompilatorze.

Do testów wybrałam język Python oraz kompilator Eclipse.

Problem:

Znaleźć minimalny i maksymalny element w tablicy n-elementowej.

Można to zrobić na 2 sposoby:

1) przechodząc po kolei po każdym elemencie tablicy zadecydować, czy przypisać go do min lub max. Złożoność tego algorytmu to ok. 2n

2) porównywać ze sobą dwa kolejne elementy i zadecydować który przypisać do min a który do max. Złożoność tego algorytmu to ok. 3*n/2 = 1,5n

Jak wynika ze wstępnych założeń, algorytm drugi powinien być o ok. 25% szybszy niż pierwszy.

Zapis w Pythonie:

Algorytm 1:

   def algorytm1(tab):

        min = 0
        max = 0
        t1 = time.clock()

        for i in range(0,ilosc,1):
            if (tab[i] > max):
                max = tab[i]
            if (tab[i] < min):
                min = tab[i]
        t2 = time.clock()

        return t2-t1

Algorytm 2:

   def algorytm2(tab):

        min = 0
        max = 0
        t1 = time.clock()

        for i in range(0,ilosc,2):
            if(tab[i] > tab[i+1]):
                if (tab[i] > max):
                    max = tab[i]
                if (tab[i+1] < min):
                    min = tab[i+1]
            else:
                if (tab[i+1] > max):
                    max = tab[i+1]
                if (tab[i] < min):
                    min = tab[i]
        t2 = time.clock()

        return t2-t1

Obie funkcje zwracają różnicę czasu pomiędzy momentem swojego startu i zakończenia.

Tablice testową program tworzy z losowo wybranych liczb typu całkowitego z przedziału od 1 do 1000. Wielkość tablicy przekazywana jest jako parametr tej funkcji.

   def genTab(ilo):

        tablica = []

        for i in range(ilo):
            tablica.append(round(random.random() * 1000))

        return tablica
 

Program zwraca procentową różnicę czasu działania między algorytmem drugim a pierwszym. Jest to średnia z x prób (ostatnia pętla).

Wyniki zaprezentowane są na wykresie:

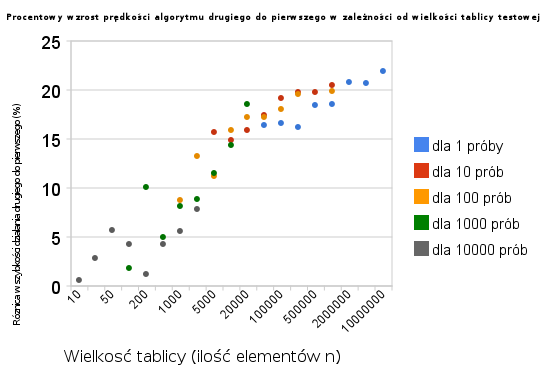
Jak widać, różnica w szybkości działania obu algorytmów jest tym bardziej widoczna, im większy jest rozmiar danych, (n-> nieskończoności).

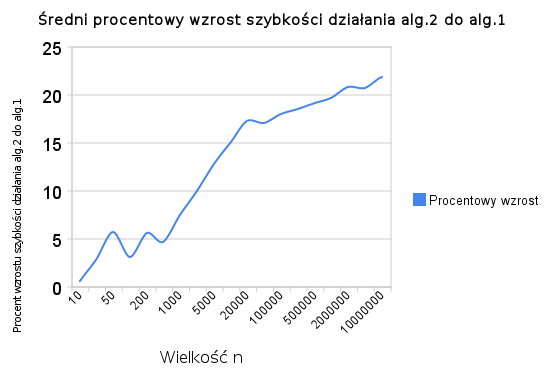
Jeszcze wykres średniej procentowej wzrostu:

A gdyby nieco zoptymalizować kod algorytmu numer 2?

Dopisałam w nim 2 linijki kodu

   zm1 = tab[i]
            zm2 = tab[i+1]

po to, aby nie odwoływać się za każdym razem do samej tablicy (która może być stosunkowo duża), zamiast tego zrobić to raz, na samym początku.

Wyniki są ciekawe:

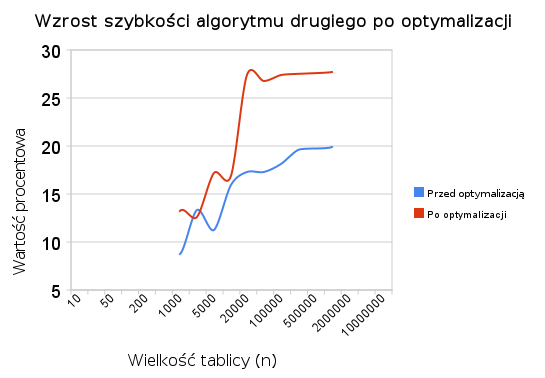
Dla dużych wartości n szybkość działania algorytmu drugiego względem pierwszego wzrosła z ok 20% do ok. 27,5% 🙂